[선형대수] 4일차 - 역행렬과 전치행렬

※ 이 글은 한양대학교 이상화교수님의 선형대수 유튜브 강의를 보며 정리한 글입니다. 잘못 이해한 부분이 있을 수도 있으니 많은 피드백 부탁드리겠습니다. 감사합니다. [유튜브 바로가기]

복습 내용

학습할 내용

1.6 中 Inverse Matrix의 조건

역행렬에 대해서 살펴봤다. 역행렬을 가지기 위한 조건을 가우스 소거법이 완료되게 하는 조건과 $det(A)\ne 0$인 조건을 통해 알아봤다. 결국엔 이 둘이 동일한 조건을 가지고 있었고, 이 동일한 조건은 다음과 같다.

$$det(a)=\prod _{i=1}^n{d}_i\ne 0$$

여기서 $d_i$는 가우스소거법의 결과로 나온 diagonal element(주대각성분)들이다.

1.6 中 Inverse Matrix의 성질

1. The inverse is unique. 행렬 A의 inverse(역행렬)가 존재할 때, 행렬 A에 대한 inverse는 딱 1개뿐이다. 이것에 대한 간단한 증명도 살펴봤다.
2. 만약 행렬 A의 역행렬이 존재한다면, $Ax=b$의 vcector X 또한 unique하다. 이는 연립방정식 양변에 역행렬을 곱해줌으로써 확인할 수 있다.
3. vector x가 non-zero이고 Ax = 0 (즉, b = 0)의 연립방정식이 성립한다면, A의 inverse는 존재하면 안된다. 그 이유는 연립방정식의 해로 vector x가 0인 것도 성립한다. 즉 System A에 들어오는 입력신호가 0인 값이 아닌 아예 없다는 뜻이다. 이를 Trivial solution이라고도 한다. 이 trivial solution이 존재할 때, vector x가 non-zero임을 가정하고 있으므로 이를 만족시키기 위해선 inverse 가 존재해선 안된다. 이유는 아래의 식에서 찾을 수 있다.
   $$\begin{array}{rl}& Ax=0(b=0)\\ & x=A^{-1}0=0\end{array}$$
   두번째 식이 만족하지 않기 위해선 행렬 A의 inverse가 존재하지 않으면 된다.
4. 2x2 행렬의 역행렬을 구하는 방식은 다음과 같다.
   $$\begin{array}{rl}& A=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\\ & A^{-1}=\frac{1}{ad-bc}\left(\begin{array}{cc}d& -b\\ -c& a\end{array}\right)\end{array}$$
   여기서 $det(A)=ad-bc$ 임을 기억하자.
5. Diagonal matrix와 그 역행렬을 살펴봤다.
   $$\begin{array}{rl}& D=\left(\begin{array}{cccc}{d}_1& 0& \cdots & 0\\ 0& d_2& \cdots & 0\\ 0& 0& \ddots & 0\\ 0& 0& \cdots & d_n\end{array}\right)\\ \\ & D^{-1}=\left(\begin{array}{cccc}\frac{1}{d_1}& 0& \cdots & 0\\ 0& \frac{1}{d_2}& \cdots & 0\\ 0& 0& \ddots & 0\\ 0& 0& \cdots & \frac{1}{d_n}\end{array}\right)\end{array}$$
6. 행렬의 곱들의 inverse는 순서를 거꾸로한 역행렬들의 곱과 같다.
   $$(ABC{)}^{-1}=C^{-1}{B}^{-1}{A}^{-1}$$
   위 식이 성립하기 위해서는 당연하게도 각 행렬들은 역행렬이 모두 존재해야 한다.

1.6 中 역행렬과 가우스 소거법

역행렬을 구하는 방법을 연립방정식을 푸는 것과 동일하게 생각할 수 있는 method이다. 이를 보기에 앞서 행렬의 곱을 행렬과 column vector들의 곱으로 나타내는 것을 다시 상기해보자.
$$\begin{array}{r}AB=A\left(\begin{array}{cccc}{b}_1& b_2& \cdots & b_n\end{array}\right)\\ =\left(\begin{array}{cccc}A{b}_1& A{b}_2& \cdots & A{b}_n\end{array}\right)\end{array}$$
위에서 $A{b}_i$는 크기가 nx1인 colomn vector와 같은 모양의 행렬이 나온다. 행렬A의 크기는 nxn, $b_1$의 크기는 nx1이라고 가정해보면, 이 둘의 곱은 column vector n개가 행렬을 이루는 모습을 생각해볼 수 있기 때문이다. 여기서 역행렬을 구해보자.
$$\begin{array}{r}A{A}^{-1}=I,A^{-1}=\left(\begin{array}{cccc}{x}_1& x_2& \cdots & x_n\end{array}\right)\\ \left(\begin{array}{cccc}A{x}_1& A{x}_2& \cdots & A{x}_n\end{array}\right)=\left(\begin{array}{cccc}1& 0& \cdots & 0\\ 0& 1& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& \cdots & 0& 1\end{array}\right)\end{array}$$
위 식에 따라서 각 $A{x}_i$는 다음의 matrix를 갖는다.
$$\begin{array}{r}A{x}_1=\left(\begin{array}{c}1\\ 0\\ 0\\ ⋮\\ 0\end{array}\right),A{x}_2=\left(\begin{array}{c}0\\ 1\\ 0\\ ⋮\\ 0\end{array}\right),\cdots \end{array}$$
이 각각의 $A{x}_i$ 꼴을 보면 이전에 배웠던 연립방정식 형태($Ax=b$)와 동일한 것을 알 수 있다. 즉, $x_i$들을 구하는 것이 역행렬을 구하는 것이고, 이 각각의 $x_i$를 구하는 것은 연립방정식을 구하는 것과 같다. 따라서 역행렬을 Gauss Elimination(가우스소거법)으로 구할 수 있는 것까지 생각해볼 수 있다. 이러한 방식보다 더 빠르게 구할 수 있는 방법, Gauss-Jordan Method가 있는데, 이를 알아보자.

1.6 中 Gauss-Jordan Method

1.6 中 Transpose Matrix

전치행렬과 대칭행렬에 대해서 살펴봤다. 행렬 A의 전치행렬을 $A^T$라고 표기하며, transpose 연산은 행렬 a의 모든 element에 대해 a_{ij}를 a_{ji}로 위치이동을 시키는 연산이다. 이 연산은 Square matrix(정방 행렬) 뿐만 아니라 Rectangular matrix도 수행이 가능하다. 이 각각의 행렬에 대해 transpose 연산을 수행하면 다음과 같이 나온다.
$$\begin{array}{rl}& \left(\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right)\stackrel{\text{transpose}}{\to }\left(\begin{array}{ccc}1& 4& 7\\ 2& 5& 8\\ 3& 6& 9\end{array}\right)\\ & \left(\begin{array}{ccc}a& b& c\\ d& e& f\end{array}\right)\stackrel{\text{transpose}}{\to }\left(\begin{array}{cc}a& d\\ b& e\\ c& f\end{array}\right)\end{array}$$

1.6 中 Transpose의 성질

1. 두 행렬의 합에 대한 전치(transpose)와 역(reverse)에 대해 살펴보면 다음과 같다.
   $$\begin{array}{rl}& (A+B{)}^T=A^T+B^T\\ & (A+B{)}^{-1}=A^{-1}+B^{-1}\end{array}$$

1.6 中 Invertible Matrix(가역 행렬)

TODO : 추후에 더 자세히 적기

n by n 행렬에 대해
가역 행렬 (invertible matrix) = 비특이 행렬 (non-singular case) = n개의 pivot을 갖는 행렬

• 모든 비특이 행렬은 가역행렬이고, 이 역 또한 참이다.
• 행렬이 invertible 하다면, 이 행렬은 n개의 pivot을 갖는다.

TODO : 추후에 더 자세히 적기

1.6 中 Symmetric Matrix

TODO : 추후에 더 자세히 적기

$$A^T=A$$ 위 식을 만족하는 행렬 A를 Symmetric Matrix, 대칭 행렬이라고 한다.

1.6 中 Correlation Matrix

$R=A^{T}A$에 대해 $R=R^T$를 만족하는 임의의 모든 행렬 R을 correlation matrix라고 한다. 여기서 말하고자 하는 것은, 대칭이 아닌 임의의 모든 행렬 (정방행렬 부터 직사각 행렬까지)에 대해 각자의 전치행렬과 행렬곱을 하여 행렬 R을 만들게 되면, 이 행렬 R은 대칭행렬이 된다는 것이다.

이 행렬 R에서 다음의 특징을 엿볼 수 있다.

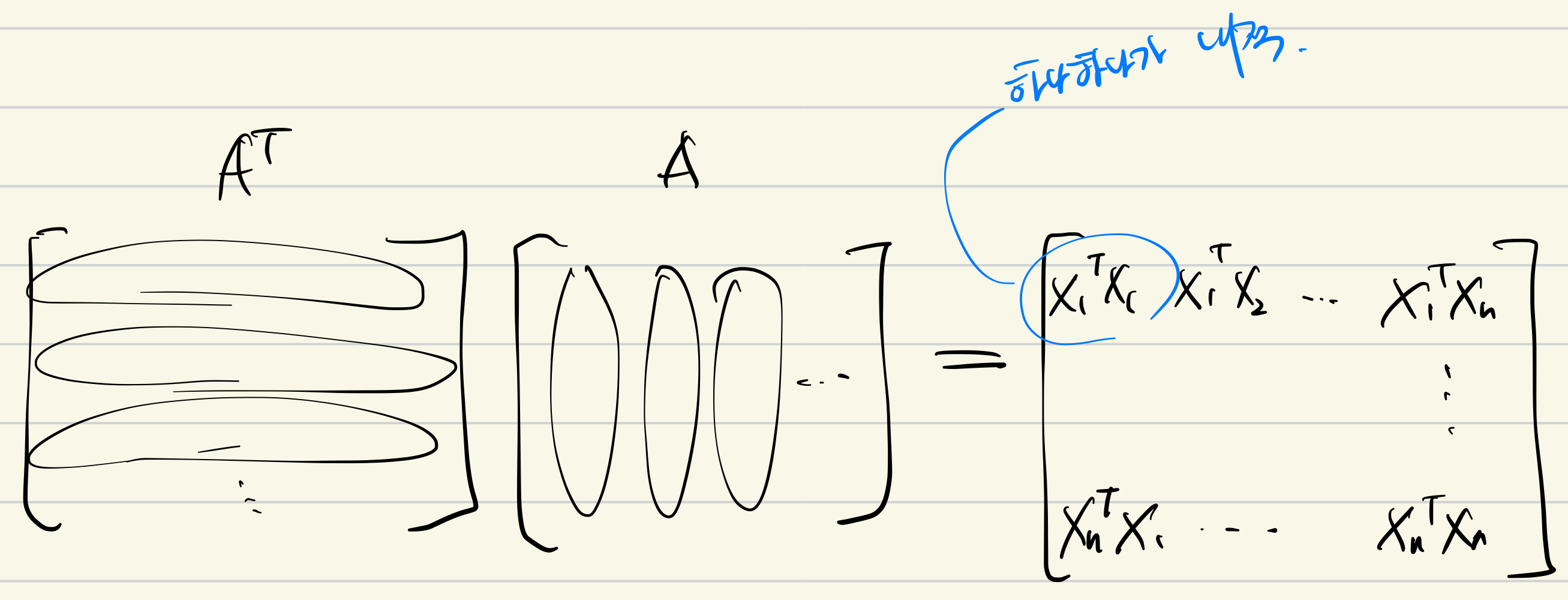
즉, correlation matrix R의 모든 성분들 하나하나가 전부 *_내적 연산_이다. 이 내적은 다음의 의미를 갖는다.

내적 : 한 vector가 다른 vector들의 성분을 얼마나 갖고 있는지에 대한 값

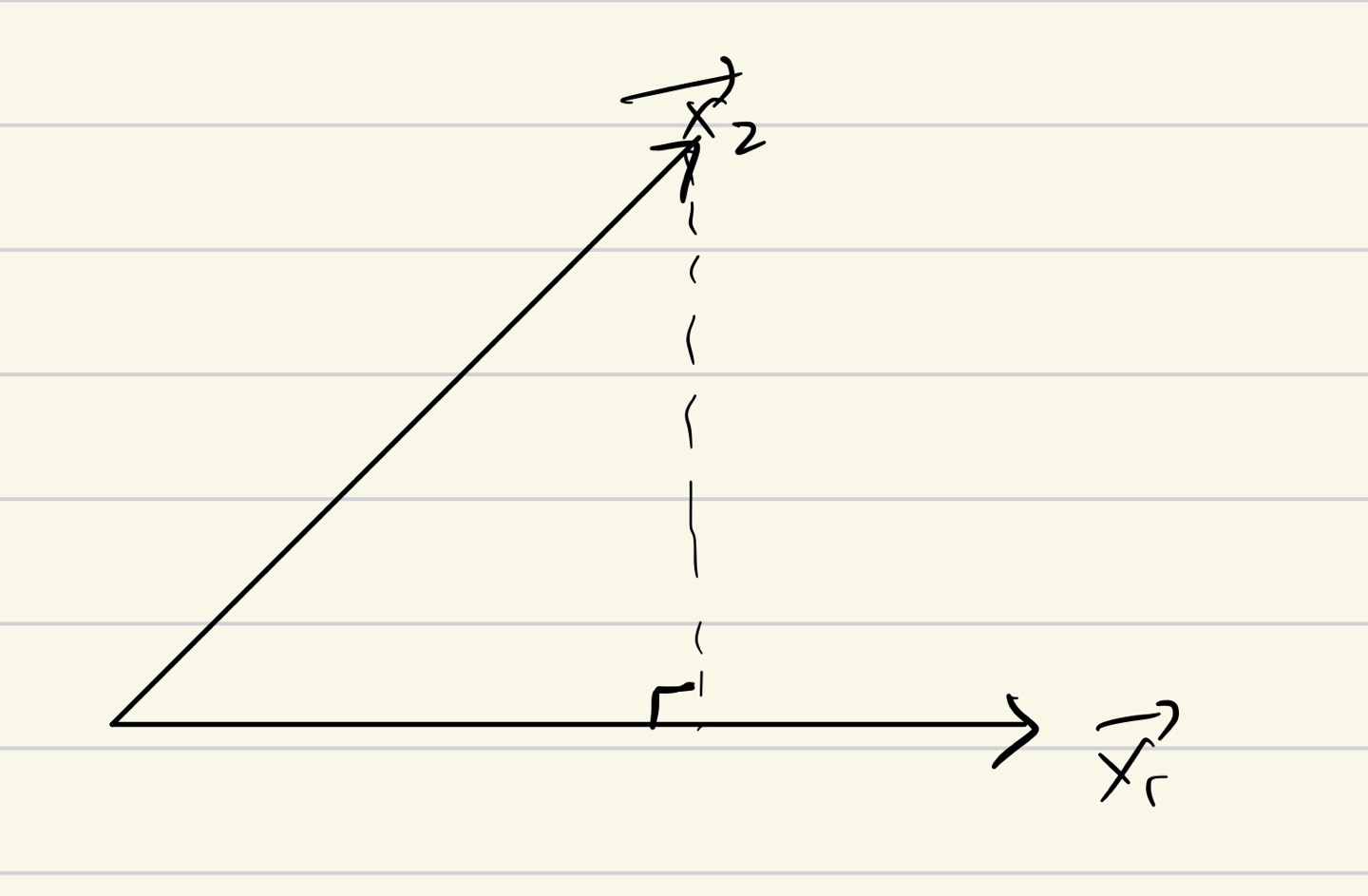
즉, 위 그림에서 살펴보자면, 벡터 x1은 벡터 x2의 성분을 얼마나 갖고 있는지를 수선의 발을 내려 그 크기를 취하고 있다. 내적은 이러한 의미를 갖는 것이다.

그럼 correlation matrix의 의미는?

한 vector가 다른 vector들의 성분을 얼마나 갖고 있는지에 조합

즉, system A에 대한 correlation matrix R을 구하게 되면, 그 벡터 공간들이 어떻게 구성되어 있는지를 알아낼 수 있다. (이 벡터 공간은 2장에서 다룰 것이다)

1.6 中 Skew-Symmetric Matrix

$$K^T=-K$$ 위 식을 만족하는 행렬 K를 Skew-Symmetric Matrix 라고 한다.